清华大学 2021 年九推机试

1、售货机

时间限制： 1.0 秒

空间限制： 512 MiB

题目描述

清华大学的自动售货机一共有 𝑛 种饮料出售，每种饮料有自己的售价，并在售货机上各有一个出售口。购买第 𝑖 种饮料时，可以在第 𝑖 个出售口支付 𝑎𝑖 的价格，售货机便会在下方的出货处放出对应的饮料。

又到了清凉的夏日，自动售货机为每种饮料各进货了1 瓶存储在其中，供同学购买。但是，自动售货机却出现了一些故障，它有可能会出货不属于这个出售口的饮料。

对于第 𝑖 个出售口，支付 𝑎𝑖 的价格购买后，如果饮料 𝑖 与饮料 𝑏𝑖 都有存货，有 𝑝𝑖 的概率出货饮料 𝑖 ，有 1−𝑝𝑖 的概率出货饮料 𝑏𝑖 。如果其中一个有存货，另一个已经没有存货，则将出货有存货的那一种饮料。如果两种饮料都没有存货，售货机将不会出货任何饮料并发出警报。**即便最后你没有获得任何饮料，也需要支付 𝑎𝑖 的价格 ** 。

长颈鹿下楼来到这台售货机前，希望能买到最近火爆全网的饮料 𝑥 ，此时售货机中 𝑛 种饮料都存货有 1 瓶。由于他知道售货机有问题，因此决定采取这样的策略来购买：

在 𝑛 个出售口中等概率选择一个出售口 𝑠 开始购买，支付这个出售口的价格 𝑎𝑠 并得到出货。
当得到想要的饮料 𝑥 时，停止购买流程，满意欢喜的离去。
当得到不想要的饮料 𝑦 时，继续在第 𝑦 个支付口购买，支付 𝑎𝑦 的价格并等待出货。
当售货机发出警报时，停止购买流程，灰心丧气的离去。

现在他希望你告诉他，他这一次购买过程期望支付的价钱数量是多少？

输入格式

从标准输入读入数据。

第一行两个正整数 𝑛,𝑥。

接下来 𝑛 行每行三个数，其中第 𝑖 行表示 𝑎𝑖,𝑏𝑖,𝑝𝑖。

输出格式

输出到标准输出。

一行一个实数表示答案，表示长颈鹿按他的策略买水期望支付的价钱。

记答案为 𝑎，而你的输出为 𝑏，那么当且仅当 |𝑎−𝑏|<10−6 时我们认为你的输出是正确的。

样例输入

2 2
8 2 0.90
7 1 0.40

样例输出

13.500000000

样例解释

售货机里饮料 1 与饮料 2 各有一瓶，且当两瓶都还有存货时，在第 1 个出售口有 0.1 的概率买到饮料 2 ，在第 2 个出售口有 0.6 的概率买到饮料 1 。

长颈鹿有0.5的概率初始选择第1个出售口开始购买，并支付8元。
有 0.1 的概率直接出货饮料 2 ，一共支付 8 元，这种情况的概率是 0.05 。
有 0.9 的概率出货饮料 1 ，则长颈鹿会再支付 8 元重新从第 1 个出售口购买饮料。由于饮料 1 已售空，第二次购买时必定直接出货饮料 2 ，一共支付 16 元，这种情况的概率是 0.45 。
长颈鹿有0.5的概率初始选择第2个出售口开始购买，并支付7元。
有 0.4 的概率直接出货饮料 2 ，一共支付 7 元，这种情况的概率是 0.2 。
有 0.6 的概率出货饮料 1 ，则长颈鹿会再支付 8 元重新从第 1 个出售口购买饮料。由于饮料 1 已售空，第二次购买时必定直接出货饮料 2 ，一共支付 15 元，这种情况的概率是 0.3 。

于是期望支付的价钱为 8×0.05+16×0.45+7×0.2+15×0.3=13.5

子任务

保证 𝑛≤2000 ， 1≤𝑏𝑖≤𝑛 , 𝑏𝑖≠𝑖 , 0≤𝑎𝑖≤100 ，0≤𝑝𝑖≤1 ，且 𝑝𝑖 不超过两位小数。

子任务 1（50分）：𝑛≤10

子任务 2（30分）：𝑝𝑖=0

子任务 3（20分）：无特殊限制

2、水滴

时间限制： 2.0 秒

空间限制： 512 MiB

相关文件： 题目目录

题目描述

这是一个经典的游戏。

在一个 𝑛×𝑚 的棋盘上，每一个格子中都有一些水滴。

玩家的操作是，在一个格子中加一滴水。

当一个格子中的水滴数超过了 4，这一大滴水就会因格子承载不住而向外扩散。扩散的规则是这样的：

这个格子中的水滴会消失，然后分别向上、左、下、右 4 个方向发射一个水滴。如果水滴碰到一个有水的格子，就会进入这个格子。否则水滴会继续移动直到到达棋盘边界后消失。扩散后，水滴进入新的格子可能导致该格子的水滴数也超过 4 ，则会立即引发这个格子的扩散。我们规定，每个格子按逆时针顺序从上方向开始，递归处理完每一个方向的扩散以及其引发的连锁反应，再处理下一个方向的扩散。

给定棋盘的初始状态和玩家的操作，求最后水滴的分布情况。

由于把水滴在一个空格看起来用处不大，所以保证所有的玩家操作都不会选择空格。

提示：可以记录每个水滴上下左右方向第一个水滴的位置，扩散时根据规则模拟，并在每次操作后维护。

输入格式

从标准输入读入数据。

第一行四个整数 𝑛,𝑚,𝑐,𝑇。

接下来 𝑐 行，每行三个正整数 𝑥𝑖,𝑦𝑖,𝑎𝑖，表示初始棋盘上第 𝑥𝑖 行 𝑦𝑖 列有 𝑎𝑖 个水滴。

接下来 𝑇 行，每行两个正整数 𝑢𝑖,𝑣𝑖，表示在第 𝑢𝑖 行 𝑣𝑖 列放入一个水滴。

输出格式

输出到标准输出。

输出 𝑇 加若干行。

前 𝑇 行每行一个整数，第 𝑖 行表示在第 𝑖 次操作后扩散的水滴数。若没有扩散输出 0。

最后若干行（可能是 0 行）表示棋盘上水滴的分布情况。由上至下，由左至右输出，每行三个正整数表示行号、列号、水滴数。

样例输入

样例输出

样例解释

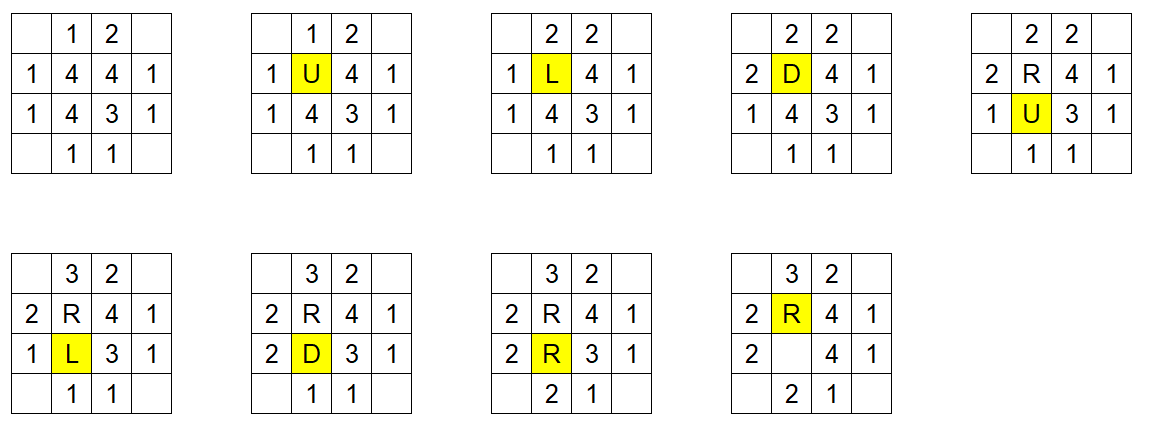
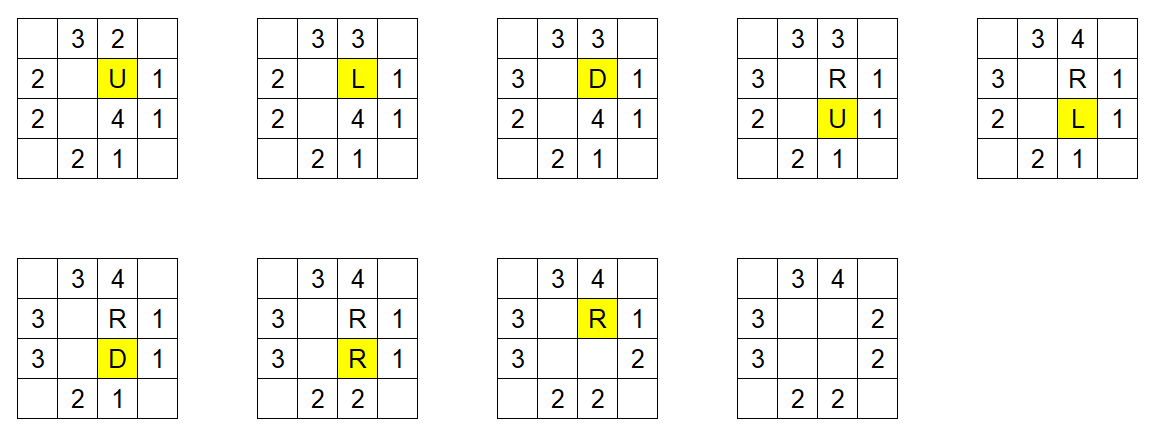
整个过程从上到下从左到右表示。

字母表示该格子即将发射水滴的方向。U：上；D：下；L：左；R：右。

黄色格子表示即将发射水滴的格子。

子任务

保证 1≤𝑛,𝑚≤351493，0≤𝑐≤750000，0≤𝑇≤500000。

保证 1≤𝑥𝑖,𝑢𝑖≤𝑛,1≤𝑦𝑖,𝑣𝑖≤𝑚,1≤𝑎𝑖≤4。

保证没有重复的 (𝑥𝑖,𝑦𝑖)。

子任务 1（17分）：𝑛,𝑚≤100

子任务 2（24分）：𝑛,𝑚≤2000

子任务 3（24分）：𝑐≤105

子任务 4（35分）：无特殊性质

3、Phi的游戏

时间限制： 1.5 秒

空间限制： 512 MiB

题目描述

Picar 和 Roman 是两个非常喜欢玩各种游戏的赌徒。这一天，他们又发现了一种新的数字游戏，名叫 𝜑 的游戏（Phigames）。

𝜑 的游戏是双人游戏，每局游戏由任意的一个正整数 𝑁 开始，由两人轮流对当前的数字进行操作。轮到其中任意一方进行操作时，玩家可以有以下三种选择：

大喊“𝜑:1！”并将当前的数字 𝑛 变为 𝜑(𝑛)；
大喊“𝜑:2！”并将当前的数字 𝑛 变为 𝜑(2𝑛)；
大喊“𝜑:𝐾！”并将当前的数字 𝑛 变为 𝜑(𝑛−𝐾)，其中 𝐾 是一个双方在开始游戏之前约定好的正整数。

其中，𝜑(𝑛) 表示的是在 1 到 𝑛 这 𝑛 个正整数中，有多少个正整数与 𝑛 互质，如 𝜑(1)=1，𝜑(4)=2，𝜑(10)=4。根据这一定义可知，𝜑(𝑛) 的定义域是 ℕ∗，所以如果选择第 3 种操作“𝜑:𝐾！”，需要保证当前的数字 𝑛>𝐾。

两名玩家轮流操作，如果谁在进行操作之后得到了已经出现过的数字，谁就输掉了本局游戏。例如，如果玩家 A 对当前的数字 1 选择了操作 1 “𝜑:1！”，由于 𝜑(1)=1 是出现过的数字，玩家 A 输掉了本局游戏，对手获胜。

𝜑 的游戏考验了玩家的心算能力和逻辑推理能力。可惜，由于 Picar 和 Roman 足够聪明，只要指定一个 𝐾 和最开始的数字 𝑁，他们就可以算出是先手还是后手有必胜策略。如果对于某个确定的 𝐾，以 𝑁 开始游戏时先手有必胜策略，则称这个 𝑁 为先手必胜态；否则后手有必胜策略，称 𝑁 为后手必胜态。为了使得这个游戏（对他们来说）更有趣，他们决定对游戏进行扩展：

玩家先指定 𝐾，并选择两个正整数 𝐿,𝑅，由系统在 [𝐿,𝑅] 中的先手必胜态中随机挑选一个 𝑟 作为右端点；
由后手选择一个正整数左端点 𝑙 ，需要保证 𝑙≤𝑟；
开始一局游戏时，系统从 [𝑙,𝑟] 中等概率挑选一个正整数 𝑁 ，作为游戏开始时由先手操作的数字。

尽管 Picar 和 Roman 足够聪明，计算修改后的游戏对他们来说也需要花费不少的时间。于是，他们找到了你，想让你帮忙计算一下修改后的游戏的平衡性。即：给定参数 𝐿,𝑅,𝐾，求后手对于任意的 𝑟 能选出最优的 𝑙 使得后手胜率最大时，先手的平均胜率。

输入格式

从标准输入读入数据。

输入仅一行，包含三个正整数 𝐿,𝑅,𝐾，含义如题目描述所示。保证 𝐿≤𝑅，且在 [𝐿,𝑅] 中至少存在一个先手必胜态。

输出格式

输出到标准输出。

输出一个实数，表示在给定的参数 𝐿,𝑅,𝐾 下，修改后的游戏的先手平均胜率。

记答案为 𝑎，而你的输出为 𝑏，那么当且仅当 |𝑎−𝑏|<10−6 时我们认为你的输出是正确的。

样例1输入

1 10 3

样例1输出

0.533333333333333333

样例1解释

此时 2,4,5,7,9,10 为先手必胜态，1,3,6,8 为后手必胜态。

𝑟=2 对应的最优左端点 𝑙 为 1，此时先手胜率为 1/2；
𝑟=4 对应的最优左端点 𝑙 为 3，此时先手胜率为 1/2；
𝑟=5 对应的最优左端点 𝑙 为 1，此时先手胜率为 3/5；
𝑟=7 对应的最优左端点 𝑙 为 6，此时先手胜率为 1/2；
𝑟=9 对应的最优左端点 𝑙 为 8，此时先手胜率为 1/2；
𝑟=10 对应的最优左端点 𝑙 为 6，此时先手胜率为 3/5。

故先手的平均胜率为 (1/2+1/2+3/5+1/2+1/2+3/5)/6=8/15≈0.5333。

样例2输入

2021 5000 0

样例2输出

0.391970630667343944

样例3输入

214 7483648 57721

样例3输出

0.490802831707061571

子任务

对于 100 的数据，保证 1≤𝐿≤𝑅≤107,0≤𝐾≤107。

具体的测试点分布见下表：

测试点	𝐿,𝑅≤	𝐾	特殊性质
1	6	<𝑅	无
2	10
3	16
4	18
5	1000
6	2000
7	3000
8	5000
9	105	𝑅−𝐿≤99
10	106	𝑅−𝐿≤9
11	5×106	=0
12	<𝑅
13	105	无
14
15
16	106	=0
17	<𝑅
18	107	𝐿=𝑅
19	无
20