清华机试真题

• 清华机试真题
  • 2017 interview
    • 轩轩
    • 旭哥
  • 2017多项式求和
    • 旭哥
    • 轩轩
  • 2018葱的战争
    • 轩轩
  • 2018路径
    • 轩轩
    • 旭哥
  • 2018四种操作
    • 波哥
    • 旭哥
    • 轩轩
  • 2021九推机试
    • 1、售货机
      • 题目描述
      • 输入格式
      • 输出格式
      • 样例输入
      • 样例输出
      • 样例解释
      • 子任务
    • 2、水滴
      • 题目描述
      • 输入格式
      • 输出格式
      • 样例输入
      • 样例输出
      • 样例解释
      • 子任务
    • 3、Phi的游戏
      • 题目描述
      • 输入格式
      • 输出格式
      • 样例1输入
      • 样例1输出
      • 样例1解释
      • 样例2输入
      • 样例2输出
      • 样例3输入
      • 样例3输出
      • 子任务

2017 interview

生活在在外星球X上的小Z想要找一些小朋友组成一个舞蹈团，于是他在网上发布了信息，一共有 \(n\) 个人报名面试。面试必须按照报名的顺序依次进行。小Z可以选择在面试完若干小朋友以后，在所有已经面试过的小朋友中进行任意顺序的挑选，以组合成一个舞蹈团。虽然说是小朋友，但是外星球X上的生态环境和地球上的不太一样，这些小朋友的身高可能相差很大。小Z希望组建的这个舞蹈团要求至少有 \(m\) 个小朋友，并且这些小朋友的最高身高和最低身高之差不能超过 \(k\) 个长度单位。现在知道了这些小朋友的身高信息，问小Z至少要面试多少小朋友才能在已经面试过的小朋友中选出不少于 \(m\) 个组成舞蹈团。

轩轩

过了14个测试点！！！

# include<algorithm>
# include<vector>
# include<iostream>
using namespace std;
typedef struct{int id;int h;} student;
bool operator <(const student& a,const student & b){return (a.h)<(b.h);}

int n,m,k,tall=0;
vector<student> stu;
vector<int> highid;
void init(){
    student temp;
    cin >> n >> m >> k;
    for(int i=0;i<n;i++){
        temp.id = i;
        cin >> temp.h;
        stu.push_back(temp);
    }
}
void pick(){
    for(int i = 0;i<=n-m;i++){ //排序
        sort(stu.begin(),stu.begin()+m+i);
        for(int j = 0;j<=i;j++){//检查个头
            if(stu[j+m-1].h-stu[j].h<=k){
                for(int y=j;y<j+m;y++){//找最大id
                    if(stu[y].id>tall) tall = stu[y].id;
                }
                cout<<tall+1<<endl;
                return;
            }
        }
    }
    cout<<"impossible"<<endl;
}
int main(){
    init();
    pick();
    return 0;
}

旭哥

测试点未通过

#include<iostream>
#include<map>
#include<list>
#include<vector>
#include<algorithm>
using namespace std;
int n,m,k;
int h;
vector<int> max_nums;
map<int,vector<int> > mp;
int main()
{
    //input
    cin>>n>>m>>k;
    for(int i = 1;i<=n;++i){
        cin>>h;
        mp[h].push_back(i);
    }
    /*operation:
    (1)统一遍历一遍面试名单：从小到大，以遇到的每个身高h为区间起点，检测在[h,h+k)这个cell中，是否能找够m：
        是:则记录下他们最大的面试者编号；放入一个记录每个小区间max_num的vector中
        否:则跳过当前，进行下一个节点循环。
    (2)扫描一遍后，输出max_num的向量中，值最小的，是他们最少需要面试的人数。
    （3）复杂度：应该是O(m*n);
    */
    map<int,vector<int> >::iterator it1 = mp.begin();//用了两个指针，构造数轴上的一个小区间
    map<int,vector<int> >::iterator it2 = it1;
    for(;it1!=mp.end();++it1){
        int counts = 0;
        int max_num = -1;
        bool enough_flag = false;
        int min_high = it1->first;//记录检测小cell中的最小身高（即基准身高），与其他身高之差，应不大于k
        for(it2 = it1;it2!=mp.end();++it2){
            if(it2->first - min_high <= k && counts <= m){
                counts += it2->second.size();
                if(it2->second[it2->second.size()-1] > max_num ){
                    max_num = it2->second[it2->second.size()-1];
                }
            }else if(counts == m) {
                enough_flag = true;
                break;
            }else  break;
        }
        if(max_num !=-1 && enough_flag ==true ) max_nums.push_back(max_num);
     }
     //搜索结束，找到所有小区间上的最小的编号
     int i= max_nums.size();
     vector<int>::iterator it3 = max_nums.begin();
     sort(it3,it3+i);
     if(!max_nums.empty()){
        cout<<max_nums.front()<<endl;
     }else
        cout<<"impossible"<<endl;
    return 0;
}

2017多项式求和

小K最近刚刚习得了一种非常酷炫的多项式求和技巧，可以对某几类特殊的多项式进行运算。非常不幸的是，小K发现老师在布置作业时抄错了数据，导致一道题并不能用刚学的方法来解，于是希望你能帮忙写一个程序跑一跑。给出一个 \(m\) 阶多项式\(\(f(x)=\sum_{i=0}^mb_ix^i\)\)对给定的正整数 \(a\) ，求\(\(S(n)=\sum_{k=0}^na^kf(k)\)\)由于这个数可能比较大，所以你只需计算 \(S(n)\) 对 \(10^9+7\) 取模后的值（即计算除以 \(10^9+7\) 后的余数）。

旭哥

只能过两个测试点！！！

#include<algorithm>
#include<cmath>
#include<stdio.h>
typedef long long ll;
using namespace std;

ll n,m,a;
int mod = 1e9+7;


//计算(a*b)%c
ll mul(ll a,ll b,ll mod) {
    ll res = 0;
    while(b > 0){
        if( (b&1) != 0)  // 二进制最低位是1 --> 加上 a的 2^i 倍, 快速幂是乘上a的2^i ）
            res  = ( res + a) % mod;
        a = (a << 1) % mod;    // a = a * 2    a随着b中二进制位数而扩大 每次 扩大两倍。
        b >>= 1;               // b -> b/2     右移  去掉最后一位 因为当前最后一位我们用完了，
    }
    return res;
}

//幂取模函数
ll pow1(ll a,ll n,ll mod){
    ll res = 1;
    while(n > 0){
        if(n&1)
            res = (res * a)%mod;
        a = (a * a)%mod;
        n >>= 1;
    }
    return res;
}


// 计算 ret = (a^n)%mod
ll pow2(ll a,ll n,ll mod) {
    ll res = 1;
    while(n > 0) {
        if(n & 1)
            res = mul(res,a,mod);
        a = mul(a,a,mod);
        n >>= 1;
    }
    return res;
}

//递归分治法求解
ll pow3(ll a,ll n,ll Mod){
    if(n == 0)
        return 1;
    ll halfRes = pow1(a,n/2,Mod);
    ll res = (ll)halfRes * halfRes % Mod;
    if(n&1)
        res = res * a % Mod;
    return res;
}

ll fun(ll b[],ll x)
{
    ll fx = 0;
    for(ll i = 0;i <= m;++i){
        fx +=  mul(b[i],pow3(x,i,mod),mod);
    }
    return fx;
}

ll Sum(ll a,ll n,ll b[])
{
    ll sum=0;
    for(ll i = 0;i <= n;++i){
        sum += mul(pow3(a,i,mod),fun(b,i),mod);
    }
    return sum%mod;
}

int main()
{
    //input:
    ll temp;
    //cin>>n>>m>>a;
    scanf("%lld %lld %lld",&n,&m,&a);
    ll b[m+1];
    for(ll i = 0;i <= m;++i){
        scanf("%lld",&b[i]);
    }
    printf("%lld",Sum(a,n,b));
    //cout<<Sum(a,n,b)<<endl;
    return 0;
}

轩轩

只能过两个测试点！！！

# include <stdio.h>
# include <iostream>
# define  MAX 1000000007
# define ll long long

using namespace std;

ll n,m,a,*b;


long long mul(long long a,long long b,long long mod) {
    long long res = 0;
    while(b > 0){
        if( (b&1) != 0)  // 二进制最低位是1 --> 加上 a的 2^i 倍, 快速幂是乘上a的2^i ）
            res  = ( res + a) % mod;
        a = (a << 1) % mod;    // a = a * 2    a随着b中二进制位数而扩大 每次 扩大两倍。
        b >>= 1;               // b -> b/2     右移  去掉最后一位 因为当前最后一位我们用完了，
    }
    return res;
}



long long pow(long long a,long long n,long long mod) {
    long long res = 1;
    while(n > 0) {
        if(n & 1)
            res = mul(res,a,mod);
        a = mul(a,a,mod);
        n >>= 1;
    }
    return res;
}


void init(){
    cin>>n>>m>>a;
    b = new ll[m+1];
    for(ll i=0;i<=m;i++){
    cin>>b[i];
    }
}


ll f(ll x){
    ll result=0;
    for(ll i=0;i<=m;i++){
        result+=mul(b[i],pow(x,i,MAX),MAX);
        result%=MAX;
    }
    return result;
}

ll s(){
    ll result=0;
    for(ll i = 0;i<=n;i++){
        result+=mul(pow(a,i,MAX),f(i),MAX);
        result%=MAX;
    }
    return result;
}

int main(){
    init();
    cout<<s()<<endl;
    return 0;
}

2018葱的战争

一个n乘m的棋盘，上面有k根葱，每根葱面朝方向为d（0123分别表示上下左右），没跟葱一个战斗力f。每隔时间葱会向面朝方向走一格，如果遇到棋盘边界，那么他将把面朝方向转180度（此回合葱不会走动），如果某个时刻有两个或以上的葱在同一位置，那么他们将发生战争，只有战斗力最高的葱存活，其他的葱全部原地枯萎，不在走动，求经过t时间后所有葱的位置

输入：第一行n m k，然后接下来k行每根葱的信息x y d f（坐标，方向，战斗力），最后一行输入时间t 输出：k行，分别表示每个葱的位置。 数据范围：n和m在100内，k在1000内，t在1000内，f在1000内，保证初始每颗葱位置不同，战斗力不同。

轩轩

以下代码测试点通过

# include<iostream>
# include<map>
# include<vector>
using namespace std;
typedef struct{int x,y;} position;
typedef struct{int id,f;} idfight;
typedef struct{int id;position p;int d;int f;bool live;} cong;
typedef vector<cong> conglist;
conglist all_cong;
map<int,vector<idfight> >war_map;
int n,m,k,times;
void init(){
    cin>>n>>m>>k;
    for(int i=0;i<n;i++){
        int x,y,d,f;
        cin >> x >>y>>d>>f;
        cong c1 ={i,{x,y},d,f,1};
        all_cong.push_back(c1);
    }
    cin >> times;
}
void action(cong &c){
    if(c.live){
    switch(c.d){
    case 0: if(c.p.y==m) c.d=1;else c.p.y++;break;
    case 1: if(c.p.y==1) c.d=0;else c.p.y--;break;
    case 2: if(c.p.x==1) c.d=3;else c.p.x--;break;
    case 3: if(c.p.y==n) c.d=2;else c.p.x++;break;
    default:;break;
    }
    int pi = c.p.x*1000+c.p.y;
    idfight idf = {c.id,c.f};
    war_map[pi].push_back(idf);
    }
}
void printans(){
        for(vector<cong>::iterator i = all_cong.begin();i!=all_cong.end();i++)  
        cout<<(*i).p.y<<" "<<(*i).p.x<<endl;
}
void fight(){
    map<int,vector<idfight> >::iterator it;
    it = war_map.begin();
    while(it!=war_map.end()){
        if((*it).second.size()>1){
            int max = 0;
            for(vector<idfight>::iterator i = (*it).second.begin();i!=(*it).second.end();i++){      
                if((*i).f>max)max = (*i).f;
            }
            for(vector<idfight>::iterator i = (*it).second.begin();i!=(*it).second.end();i++){      
                if((*i).f<max) all_cong[(*i).id].live=0;
            }
        }
    it++;
    }
}
int main() {
    init();
    while(times--){
    for(vector<cong>::iterator i = all_cong.begin();i!=all_cong.end();i++){     
        action(*i);
    }
    fight();
    war_map.clear();
    }
    printans();
    return 0;
}

2018路径

有n个点，每个点有一个权值，每两点间的不同边的个数为他们权值相与得到的值的二进制数字中的1的个数（边为有向边，有第i指向第j，i小于j）求第1个点到第n个点的路径个数（当且仅当不止一条边不同才被称为两条不同的路径），由于数据很大，对991247取模。

输入：第1行n，第二行分别试每个点权值 输出：路径个数 数据范围:n在2e5内，权值大小在1e9内

轩轩

# include<iostream>
# include<bitset>
# include<vector>
# define MAX_BIT 32
using namespace std;
vector<int> power; 
int n;
void init(){
    cin>>n;
    for(int i=0;i<n;i++){
        int temp;
        cin>>temp;
        power.push_back(temp);
    }
}
int countones(int a,int b){
    int c = a&b;
    bitset<MAX_BIT> bt(c);
    return bt.count();
}
int calc(int n){
    return n==1?
    countones(power[0],power[1]):
    countones(power[0],power[n])+
    calc(n-1)*countones(power[n],power[n-1])%991127;
}
int main(){
    init();
    cout<<calc(n-1)%991127<<endl;
    return 0;
}

旭哥

以下代码测试点通过

#include<iostream>
using namespace std;
struct Node
{
    int n;
    int w;
}node[200003];
int countOnes(int a,int b)
{
    //count the number in the ans(&)
    int c = a&b;
    int ones = 0;
    while(c != 0){
        if(c%2 == 1)
            ones++;
        c = c>>1;
    }
    return ones;
}

int Routes(int n)
{
    if(n == 1 || n==0 )
        return 0;
    else if(n > 1)
        return countOnes(1,n) + Routes(n-1)*countOnes(n-1,n);
}
int main()
{
    int n,f,routes = 0;
    cin>>n;
    for(int i = 1;i <= n;++i){
        cin>>f;
        node[i].n = i;
        node[i].w= f;
    }
    routes = Routes(5);
    cout<<routes<<endl;
    return 0;

}

2018四种操作

有一个n个元素的数列,元素的值只能是0 1 2三个数中的一个，定义四种操作，(1 i x)表示为把第i位替换成x，x也只能是0 1 2三个数中的一个，(2 i j)表示把第i个数到第j个数所有的元素值加1，并对3取模，(3 i j)表示把第i个数到第j个数之间的序列的颠倒顺序，(4 i j)表示查询第i个数到第j个数之间的序列是否存在三个或以上相同数，如果有，输出yes，否则输出no

输入：第一行输入n，接下来一行输入n个数，保证是0 1 2中的一个，第三行输入一个数q，表示操作个数，接下来q行输入q种操作 输出：每次第四次操作时，输出yes或者no 数据范围：不记得了

波哥

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[100000];
void replace(int a[],int i,int x ){
     a[i-1]=x;
}

void addx_y(int a[],int x,int y){
    for(int i=x-1;i<y;i++){
       a[i]=(a[i]+1)%3;
    }
}
void ser_com3(int a[],int x,int y){
    int zeros=0;
    int ones=0;
    int twos=0;
    bool flag=0;
    for(int k=x-1;k<y;k++){
       if(a[k]==0)zeros++;
       if(a[k]==1)ones++;
       if(a[k]==2)twos++;
       if(zeros>=3||ones>=3||twos>=3){
           flag=1;
           cout<<"yes"<<endl;
           break;
       }
    }
    if(!flag)cout<<"no"<<endl;
}

int main(){
    int n;
    int op,x,y;
    while(scanf("%d",&n)!=EOF){
        for(int i=0;i<n;i++)scanf("%d",&a[i]);
        int q;
        cin>>q;
        while(q--){
            cin>>op>>x>>y;
            switch(op){
                case 1: replace(a,x,y);
                case 2: addx_y(a,x,y);
                case 3: reverse(a+x-1,a+y);
                case 4: ser_com3(a,x,y);
                default:break;
            }
        }
    }
    return 0;
}

旭哥

#include<iostream>
using namespace std;

int a[10000001];
void rep(int a[],int i,int e)
{
    a[i] = e;
}

void addall(int a[],int i,int j)
{
    for(int k = i;k <= j;++k){
        a[k] = (a[k]+1)%3;
    }
}

void rev(int a[],int i,int j)
{
    int temp;
    if((j-i)%2 == 0){
        for(int k = i,m = j;k != m ;++k,--m){
            temp = a[k];
            a[k] = a[m];
            a[m] = temp;
        }
    }else{
        for(int k = i,m = j;k != m-1 ;++k,--m){
            temp = a[k];
            a[k] = a[m];
            a[m] = temp;
        }
    }
}

void quire(int a[],int i,int j)
{
    int zeros,ones,twos;
    for(int k = i;k<j;++k){
        if(a[k] == 0)
            zeros++;
        else if(a[k] == 1)
            ones++;
        else if(a[k] == 2)
            twos++;
        if(zeros >= 3||ones >= 3 || twos >= 3){
            cout<<"yes"<<endl;
            break;
        }
    }
    cout<<"no"<<endl;
}

int main()
{
    int n,q,x,op,s,e;

    //input
    for(int i = 0;i<n;++i){
        cin>>x;
        a[i] = x;
    }
    cin>>q;
    for(int i = 0;i < q ;++i){
        cin>>op>>s>>e;
        if(s == 1)
            rep(a,s,e);
        else if(s == 2)
            addall(a,s,e);
        else if(s == 3 )
            rev(a,s,e);
        else if(s == 4 )
            quire(a,s,e);
    }

    return 0;
}

轩轩

# include<iostream>
# include<vector>
# include<algorithm>
using namespace std;

typedef struct {int x,y,z;} comm;
vector<int> numlist;
vector<comm> commlist;
int n,q;

void init(){
    int temp;
    cin>>n;
    while(n--){
        cin>>temp;
        numlist.push_back(temp);
    }
    cin>>q;
    int x,y,z;
    while(q--){
        cin>>x>>y>>z;
        comm command = {x,y,z};
        commlist.push_back(command);
    }
}
void printdata(){
    vector<int>::iterator it;
    it = numlist.begin();
    while(it!=numlist.end()){
    cout<<(*it)<<" ";
    it++;
    }
    cout<<endl;
}
void action_1(int i,int x){
    numlist[i-1]=x;
}

void action_2(int i ,int j){
    i--;j--;
    for(;i<=j;i++){
        numlist[i]=(numlist[i]+1)%3;
    }

}
void action_3(int i ,int j){
    i--;
    reverse(numlist.begin()+i,numlist.begin()+j);

}
void action_4(int i , int j){
    i--;
    int a,b,c;
    a =  count(numlist.begin()+i,numlist.begin()+j,0);
    b =  count(numlist.begin()+i,numlist.begin()+j,1);
    c =  count(numlist.begin()+i,numlist.begin()+j,2);
    if((a>2)||(b>2)||(c>2))cout<<"yes"<<endl;
    else cout<<"no"<<endl;
}
int main(){
    init();
    vector<comm>::iterator i;
    i = commlist.begin();
    while(i!=commlist.end()){
        switch((*i).x){
        case 1:action_1((*i).y,(*i).z);break;
        case 2:action_2((*i).y,(*i).z);break;
        case 3:action_3((*i).y,(*i).z);break;
        case 4:action_4((*i).y,(*i).z);break;
        default:;
        }
    i++;
    }
    printdata();
    return 0;
}

2021九推机试

1、售货机

时间限制： 1.0 秒

空间限制： 512 MiB

题目描述

清华大学的自动售货机一共有 𝑛 种饮料出售，每种饮料有自己的售价，并在售货机上各有一个出售口。购买第 𝑖 种饮料时，可以在第 𝑖 个出售口支付 𝑎𝑖 的价格，售货机便会在下方的出货处放出对应的饮料。

又到了清凉的夏日，自动售货机为每种饮料各进货了1 瓶存储在其中，供同学购买。但是，自动售货机却出现了一些故障，它有可能会出货不属于这个出售口的饮料。

对于第 𝑖 个出售口，支付 𝑎𝑖 的价格购买后，如果饮料 𝑖 与饮料 𝑏𝑖 都有存货，有 𝑝𝑖 的概率出货饮料 𝑖 ，有 1−𝑝𝑖 的概率出货饮料 𝑏𝑖 。如果其中一个有存货，另一个已经没有存货，则将出货有存货的那一种饮料。如果两种饮料都没有存货，售货机将不会出货任何饮料并发出警报。**即便最后你没有获得任何饮料，也需要支付 𝑎𝑖 的价格 ** 。

长颈鹿下楼来到这台售货机前，希望能买到最近火爆全网的饮料 𝑥 ，此时售货机中 𝑛 种饮料都存货有 1 瓶。由于他知道售货机有问题，因此决定采取这样的策略来购买：

• 在 𝑛 个出售口中等概率选择一个出售口 𝑠 开始购买，支付这个出售口的价格 𝑎𝑠 并得到出货。
• 当得到想要的饮料 𝑥 时，停止购买流程，满意欢喜的离去。
• 当得到不想要的饮料 𝑦 时，继续在第 𝑦 个支付口购买，支付 𝑎𝑦 的价格并等待出货。
• 当售货机发出警报时，停止购买流程，灰心丧气的离去。

现在他希望你告诉他，他这一次购买过程期望支付的价钱数量是多少？

输入格式

从标准输入读入数据。

第一行两个正整数 𝑛,𝑥。

接下来 𝑛 行每行三个数，其中第 𝑖 行表示 𝑎𝑖,𝑏𝑖,𝑝𝑖。

输出格式

输出到标准输出。

一行一个实数表示答案，表示长颈鹿按他的策略买水期望支付的价钱。

记答案为 𝑎，而你的输出为 𝑏，那么当且仅当 |𝑎−𝑏|<10−6 时我们认为你的输出是正确的。

样例输入

2 2
8 2 0.90
7 1 0.40

样例输出

13.500000000

样例解释

售货机里饮料 1 与饮料 2 各有一瓶，且当两瓶都还有存货时，在第 1 个出售口有 0.1 的概率买到饮料 2 ，在第 2 个出售口有 0.6 的概率买到饮料 1 。

• 长颈鹿有0.5的概率初始选择第1个出售口开始购买，并支付8元。
• 有 0.1 的概率直接出货饮料 2 ，一共支付 8 元，这种情况的概率是 0.05 。
• 有 0.9 的概率出货饮料 1 ，则长颈鹿会再支付 8 元重新从第 1 个出售口购买饮料。由于饮料 1 已售空，第二次购买时必定直接出货饮料 2 ，一共支付 16 元，这种情况的概率是 0.45 。
• 长颈鹿有0.5的概率初始选择第2个出售口开始购买，并支付7元。
• 有 0.4 的概率直接出货饮料 2 ，一共支付 7 元，这种情况的概率是 0.2 。
• 有 0.6 的概率出货饮料 1 ，则长颈鹿会再支付 8 元重新从第 1 个出售口购买饮料。由于饮料 1 已售空，第二次购买时必定直接出货饮料 2 ，一共支付 15 元，这种情况的概率是 0.3 。

于是期望支付的价钱为 8×0.05+16×0.45+7×0.2+15×0.3=13.5

子任务

保证 𝑛≤2000 ， 1≤𝑏𝑖≤𝑛 , 𝑏𝑖≠𝑖 , 0≤𝑎𝑖≤100 ，0≤𝑝𝑖≤1 ，且 𝑝𝑖 不超过两位小数。

子任务 1（50分）：𝑛≤10

子任务 2（30分）：𝑝𝑖=0

子任务 3（20分）：无特殊限制

2、水滴

时间限制： 2.0 秒

空间限制： 512 MiB

相关文件： 题目目录

题目描述

这是一个经典的游戏。

在一个 𝑛×𝑚 的棋盘上，每一个格子中都有一些水滴。

玩家的操作是，在一个格子中加一滴水。

当一个格子中的水滴数超过了 4，这一大滴水就会因格子承载不住而向外扩散。扩散的规则是这样的：

这个格子中的水滴会消失，然后分别向上、左、下、右 4 个方向发射一个水滴。如果水滴碰到一个有水的格子，就会进入这个格子。否则水滴会继续移动直到到达棋盘边界后消失。扩散后，水滴进入新的格子可能导致该格子的水滴数也超过 4 ，则会立即引发这个格子的扩散。我们规定，每个格子按逆时针顺序从上方向开始，递归处理完每一个方向的扩散以及其引发的连锁反应，再处理下一个方向的扩散。

给定棋盘的初始状态和玩家的操作，求最后水滴的分布情况。

由于把水滴在一个空格看起来用处不大，所以保证所有的玩家操作都不会选择空格。

提示：可以记录每个水滴上下左右方向第一个水滴的位置，扩散时根据规则模拟，并在每次操作后维护。

输入格式

从标准输入读入数据。

第一行四个整数 𝑛,𝑚,𝑐,𝑇。

接下来 𝑐 行，每行三个正整数 𝑥𝑖,𝑦𝑖,𝑎𝑖，表示初始棋盘上第 𝑥𝑖 行 𝑦𝑖 列有 𝑎𝑖 个水滴。

接下来 𝑇 行，每行两个正整数 𝑢𝑖,𝑣𝑖，表示在第 𝑢𝑖 行 𝑣𝑖 列放入一个水滴。

输出格式

输出到标准输出。

输出 𝑇 加若干行。

前 𝑇 行每行一个整数，第 𝑖 行表示在第 𝑖 次操作后扩散的水滴数。若没有扩散输出 0。

最后若干行（可能是 0 行）表示棋盘上水滴的分布情况。由上至下，由左至右输出，每行三个正整数表示行号、列号、水滴数。

样例输入

4 4 12 1
1 2 1
1 3 2
2 1 1
2 4 1
3 1 1
3 4 1
4 2 1
4 3 1
2 2 4
2 3 4
3 2 4
3 3 3
2 2

样例输出

4
1 2 3
1 3 4
2 1 3
2 4 2
3 1 3
3 4 2
4 2 2
4 3 2

样例解释

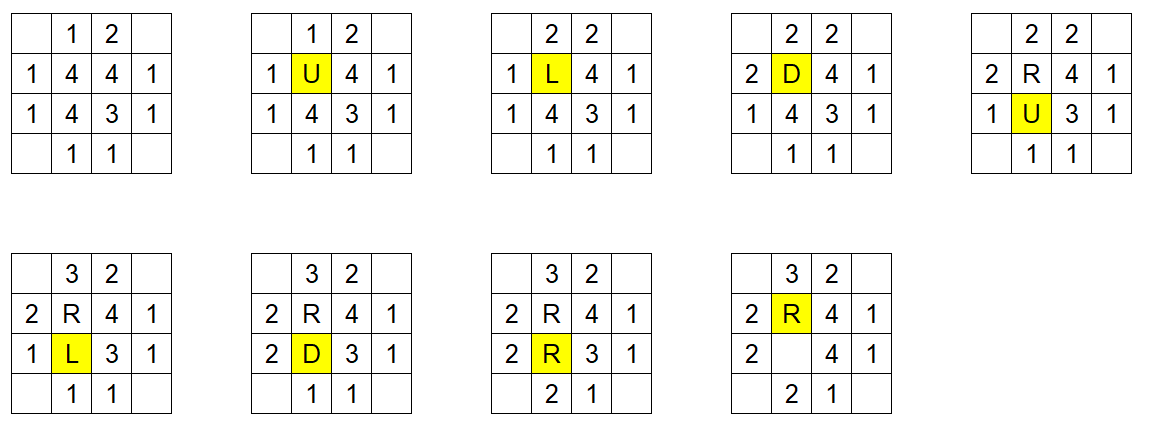
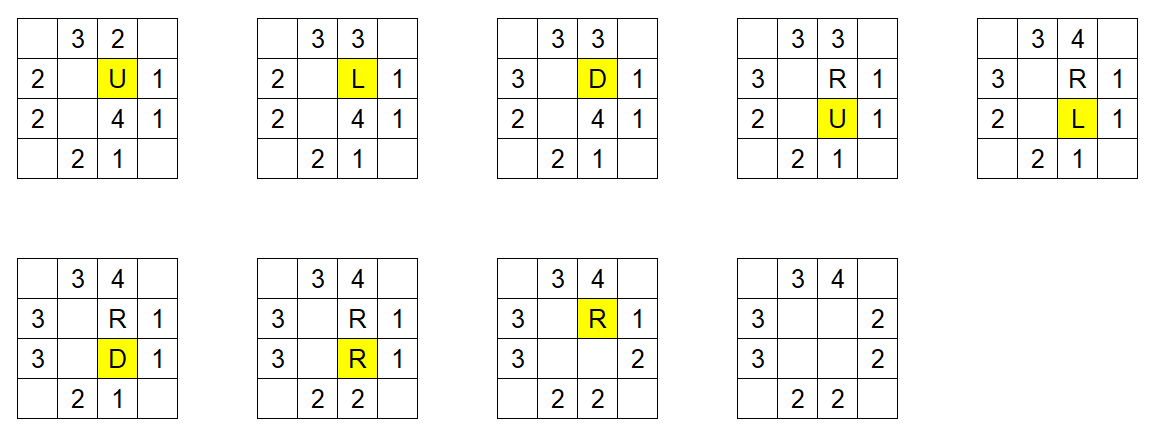
整个过程从上到下从左到右表示。

字母表示该格子即将发射水滴的方向。U：上；D：下；L：左；R：右。

黄色格子表示即将发射水滴的格子。

子任务

保证 1≤𝑛,𝑚≤351493，0≤𝑐≤750000，0≤𝑇≤500000。

保证 1≤𝑥𝑖,𝑢𝑖≤𝑛,1≤𝑦𝑖,𝑣𝑖≤𝑚,1≤𝑎𝑖≤4。

保证没有重复的 (𝑥𝑖,𝑦𝑖)。

子任务 1（17分）：𝑛,𝑚≤100

子任务 2（24分）：𝑛,𝑚≤2000

子任务 3（24分）：𝑐≤105

子任务 4（35分）：无特殊性质

3、Phi的游戏

时间限制： 1.5 秒

空间限制： 512 MiB

题目描述

Picar 和 Roman 是两个非常喜欢玩各种游戏的赌徒。这一天，他们又发现了一种新的数字游戏，名叫 𝜑 的游戏（Phigames）。

𝜑 的游戏是双人游戏，每局游戏由任意的一个正整数 𝑁 开始，由两人轮流对当前的数字进行操作。轮到其中任意一方进行操作时，玩家可以有以下三种选择：

1. 大喊“𝜑:1！”并将当前的数字 𝑛 变为 𝜑(𝑛)；
2. 大喊“𝜑:2！”并将当前的数字 𝑛 变为 𝜑(2𝑛)；
3. 大喊“𝜑:𝐾！”并将当前的数字 𝑛 变为 𝜑(𝑛−𝐾)，其中 𝐾 是一个双方在开始游戏之前约定好的正整数。

其中，𝜑(𝑛) 表示的是在 1 到 𝑛 这 𝑛 个正整数中，有多少个正整数与 𝑛 互质，如 𝜑(1)=1，𝜑(4)=2，𝜑(10)=4。根据这一定义可知，𝜑(𝑛) 的定义域是 ℕ∗，所以如果选择第 3 种操作“𝜑:𝐾！”，需要保证当前的数字 𝑛>𝐾。

两名玩家轮流操作，如果谁在进行操作之后得到了已经出现过的数字，谁就输掉了本局游戏。例如，如果玩家 A 对当前的数字 1 选择了操作 1 “𝜑:1！”，由于 𝜑(1)=1 是出现过的数字，玩家 A 输掉了本局游戏，对手获胜。

𝜑 的游戏考验了玩家的心算能力和逻辑推理能力。可惜，由于 Picar 和 Roman 足够聪明，只要指定一个 𝐾 和最开始的数字 𝑁，他们就可以算出是先手还是后手有必胜策略。如果对于某个确定的 𝐾，以 𝑁 开始游戏时先手有必胜策略，则称这个 𝑁 为先手必胜态；否则后手有必胜策略，称 𝑁 为后手必胜态。为了使得这个游戏（对他们来说）更有趣，他们决定对游戏进行扩展：

• 玩家先指定 𝐾，并选择两个正整数 𝐿,𝑅，由系统在 [𝐿,𝑅] 中的先手必胜态中随机挑选一个 𝑟 作为右端点；
• 由后手选择一个正整数左端点 𝑙 ，需要保证 𝑙≤𝑟；
• 开始一局游戏时，系统从 [𝑙,𝑟] 中等概率挑选一个正整数 𝑁 ，作为游戏开始时由先手操作的数字。

尽管 Picar 和 Roman 足够聪明，计算修改后的游戏对他们来说也需要花费不少的时间。于是，他们找到了你，想让你帮忙计算一下修改后的游戏的平衡性。即：给定参数 𝐿,𝑅,𝐾，求后手对于任意的 𝑟 能选出最优的 𝑙 使得后手胜率最大时，先手的平均胜率。

输入格式

从标准输入读入数据。

输入仅一行，包含三个正整数 𝐿,𝑅,𝐾，含义如题目描述所示。保证 𝐿≤𝑅，且在 [𝐿,𝑅] 中至少存在一个先手必胜态。

输出格式

输出到标准输出。

输出一个实数，表示在给定的参数 𝐿,𝑅,𝐾 下，修改后的游戏的先手平均胜率。

记答案为 𝑎，而你的输出为 𝑏，那么当且仅当 |𝑎−𝑏|<10−6 时我们认为你的输出是正确的。

样例1输入

1 10 3

样例1输出

0.533333333333333333

样例1解释

此时 2,4,5,7,9,10 为先手必胜态，1,3,6,8 为后手必胜态。

• 𝑟=2 对应的最优左端点 𝑙 为 1，此时先手胜率为 1/2；
• 𝑟=4 对应的最优左端点 𝑙 为 3，此时先手胜率为 1/2；
• 𝑟=5 对应的最优左端点 𝑙 为 1，此时先手胜率为 3/5；
• 𝑟=7 对应的最优左端点 𝑙 为 6，此时先手胜率为 1/2；
• 𝑟=9 对应的最优左端点 𝑙 为 8，此时先手胜率为 1/2；
• 𝑟=10 对应的最优左端点 𝑙 为 6，此时先手胜率为 3/5。

故先手的平均胜率为 (1/2+1/2+3/5+1/2+1/2+3/5)/6=8/15≈0.5333。

样例2输入

2021 5000 0

样例2输出

0.391970630667343944

样例3输入

214 7483648 57721

样例3输出

0.490802831707061571

子任务

对于 100 的数据，保证 1≤𝐿≤𝑅≤107,0≤𝐾≤107。

具体的测试点分布见下表：

测试点	𝐿,𝑅≤	𝐾	特殊性质
1	6	<𝑅	无
2	10
3	16
4	18
5	1000
6	2000
7	3000
8	5000
9	105	𝑅−𝐿≤99
10	106	𝑅−𝐿≤9
11	5×106	=0
12	<𝑅
13	105	无
14
15
16	106	=0
17	<𝑅
18	107	𝐿=𝑅
19	无
20